|
|
|
|
|
|
Part 3: Euler's Method
We ended Part 2 with an initial value problem to be solved: Find v = v(t) so that
dv/dt = g - cv and v(0) = 0.
More generally, our problem is to solve any initial value problem of the form
dv/dt = f(t,v) with v(0) = v0.
We will calculate approximate values for the velocity v at n equally spaced points in some fixed time interval. Our procedure will be exactly like the one we developed in the Limited Population module: We will repeatedly calculate a rise in v as slope x run.
The following development is very similar to what we did in Limited Population Growth. If you understood the numerical method there, you may scan quickly through this part or skip it entirely. If you feel shaky about how we generated solutions in that module, you may benefit from studying this again.
Our goal is to estimate the velocity v(t) at times
t0 = 0, t1 = Delta-t, t2 = 2 Delta-t, ... , tn = n Delta-t.
Our estimated velocity values at these times will be denoted by
v0, v1, v2, v3, ... , vn.
Our method for estimating the velocity values will be recursive, i.e., vk will be calculated from the preceding vk-1 for each k = 1, 2, 3, ... .
How do we obtain v1 from v0, the initial velocity? We will answer this in a geometric fashion. We will look at the graph of velocity versus time on the (t,v)-plane. The first diagram ...
...shows a graph of the starting situation: the initial velocity v0 is shown as a vertical line segment of length v0 at the starting time t0 = 0. We now add ...
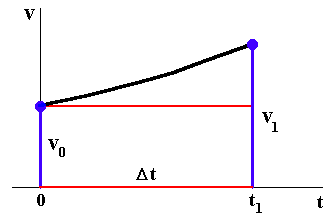
... the graph of v versus t. Our next velocity value, v1, is shown as the length of a vertical line segment at time t1. However, the value of v1 is not known to us, and hence we will estimate its value. We do this by...
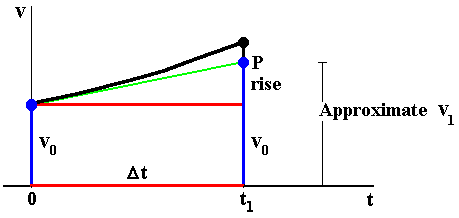
...drawing the tangent line to the graph at t = t0. Follow this tangent line to the point P, the top of a vertical line segment that approximates v1. Moreover, we can compute the length of this new line segment: We separate the line segment into two pieces -- the bottom piece having length v0 and the top piece being the rise of a right triangle with run = Delta-t. Using
slope = rise / run,
we see that rise equals slope times Delta-t. Hence, since v1 is approximated by v0 + slope x Delta-t,
v1 ~ v0 + slope x Delta-t.
(We use the symbol ~ to mean "almost equal to".)
This is the key to Euler's Method for approximating the solution of an initial value problem. It's valuable because the slope (of the tangent line) equals the derivative dv/dt, which is given by our original differential equation when t = t0 and v = v0:
slope = dv/dt = g - cv0.
Substituting this value of the slope into the preceding equation, we find
v1 ~ v0 + (g - cv0) x Delta-t.
Great! This gives us a method for going from v0 to v1. But how do we go from v1 to v2? Easy -- we use the same equation, only with v0 and v1 replaced by v1 and v2:
v2 ~ v1 + (g - cv1) x Delta-t.
In general, to go from vk-1 to vk we have
vk ~ vk-1 + (g - cvk-1) x Delta-t.
This equation, along with the initial value v0 = 0 and the assignment of a value to the step size Delta-t, plays the central role in our computations.
|
|
|
Last modified: October 14, 1997