Time and Temperature

Part 1: Background

In this module we study cyclic phenomena in our natural environment, and we explore the extent to which we can model these phenomena by trigonometric functions.

As an example, we start with sunrise and sunset data, which may be found in abundance on a web page at the U. S. Naval Observatory. Specifically, you can enter any location in the U. S. and any year, and the USNO site will generate a table of sunrise and sunset times for that location and that year. Another option will produce similar data for moonrise and moonset. So, if you don't like our choice of location or year, feel free to replace our data with data of your choice.

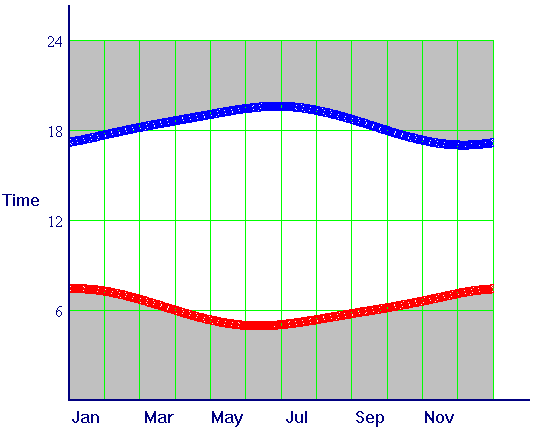
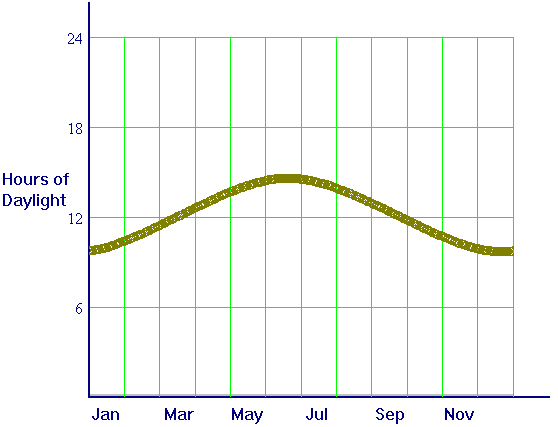
In the figure below, we show graphically the USNO data for sunrise and sunset for the 365 days of 1997 at Durham, NC. From these data, we may compute hours of sunlight in Durham (where the sun always shines, of course). We show the computed graph of daylight hours in the second figure below.

The following questions are observation and thought questions. They don't require any computation beyond visual estimates. (Computation comes in the next part.) We will refer to the two curves in the first figure as sunrise and sunset, and to the curve in the second figure as daylight.

1. How is the daylight curve computed from the sunrise and sunset curves?
2. Which one(s) of the three curves appear to be sinusoidal, that is, to have the shape of a sine curve? For any that does not look sinusoidal, describe the way in which it fails to be sinusoidal.
3. What days do you expect to be the shortest and longest (in the sense of hours of daylight)? Are these the days of earliest and latest sunrise and sunset? Explain.
4. Estimate the length of the longest day. Of the shortest day.
5. Estimate the average number of hours of daylight over the entire year.
6. Estimate the period of the daylight curve. In what way(s) would you expect a daylight curve for 1996 or 1998 to differ from that for 1997?
7. Where would you place an origin (0,0) in the date-daylight plane to make it as simple as possible to fit a sine curve to the data? That is, what date and what number of hours of daylight would give the most convenient starting point for your fitted function? Explain your answer.
8. If we leave the origin and scale where they are -- 0 date on January 1, with time measured in days or months (your choice), and daylight measured in hours from 0 -- we are likely to find a sinusoidal function of the form
   h(t) = A + B sin [ C (t - t₀)].
   Explain how A, B, C, and t₀ are related (in some order) to the lengths of longest and shortest days, the average length over a year, the period, and your choice of where to put the origin.
9. Use your answers to steps 4 through 7 to estimate the coefficients in step 8. That is, write a specific sinusoidal function that you think will match the data.

In a later part of the module, we will see that long-term average temperature data for a given location also tends to have a sinusoidal pattern.

Last modified: October 28, 1997