Complex Line Integrals I, part 1

Let f be a continuous complex-valued function of a complex variable, and let C be a smooth curve in the complex plane parametrized by

Z(t) = x(t) + i y(t) for t varying between a and b.
Then the complex line integral of f over C is given by

Note that the "smooth" condition guarantees that Z^' is continuous and, hence, that the integral exists.

We will consider line integrals of the following functions

over a varierty of different curves.

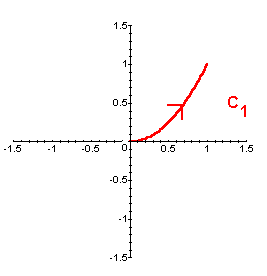
Calculate the line integral of the square function, f₂, over the curve C₁, the parabola y = x² from 0 to 1 + i, using the parametric representation

Z(t) = t + t²i for t between 0 and 1.

Repeat the calculation for the parametric representation

Z(t) = t ²+ t⁴i for t between 0 and 1.
Now repeat the calculation using your own parametric representation for C₁.
Repeat Step 1 for the function f₄.
Summarize your calculations in Steps 1 and 2.
Next we consider integrating our functions f₂ and f₄ over a number of different curves that connect 0 to 1 + i. Use the given parametric representations for the curves C₂ and C₃ to calculate the integrals

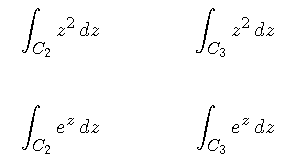
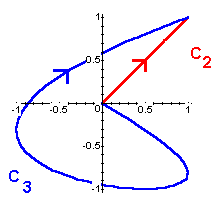
where C₂ and C₃ are the curves displayed below. Record your results. What do you observe about the values of the integrals?
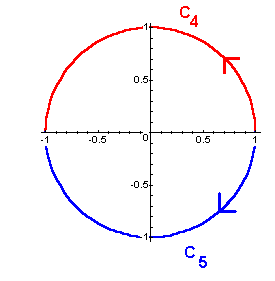
Let C₄ be the top half of the unit circle traced out from 1 to -1, and let C₅ be the bottom half of the unit circle traced out from 1 to -1.

Calculate the integrals of all four functions over each of the two curves and record your results. (Check to make sure that your parametric representations trace out the curves in the correct directions. Also check the bounds on your parametric intervals.)