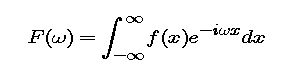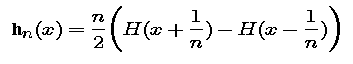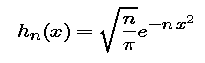Fourier Transform I
Part 1. Introduction
The Fourier transform is a useful tool in understanding problems posed by partial differential equations with unbounded spatial regions. We begin by examining the transform itself and then apply it to understanding the time evolution of temperature in an unbounded rod.
Let f be an absolutely integrable function on the real line. Then the Fourier transform F is given by
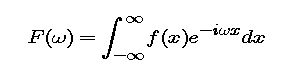
The Fourier transform is particularly well-suited to understanding problems incorporating associated conditions with discontinuities. A fundamental function used in describing such conditions is the Heaviside function.
- Use your computer algebra system to graph the Heaviside function H.
- Now graph the function H(x + 2) - H(x - 2).
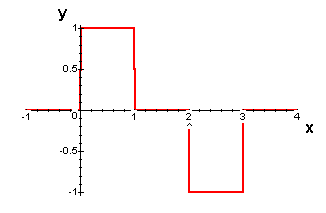
- Use the Heavisde function to construct a function with the graph shown below.
Your computer algebra system associates more information with the Heaviside function than is apparent from its graph.
- Use your computer algebra system to calculate the derivative of the Heaviside function.
The Dirac "delta function" is not really a function at all, but , as we will see below, can be thought of as the limit of a sequence of functions.
- First, calculate the integrals of the delta function over intervals of the form [-a, a], where a assumes the values 1, 1/2, 1/4, and 1/8.
So the Dirac delta "function" is nonegative with integral 1 and support concentrated at 0. It is useful to think of the delta function as the limit of a sequence hn of nonnegative functions each having integral 1 and with support shrinking down toward 0 as n increases. We'll look at two such sequences.
- Look at the graphs of
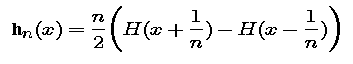
as n approaches infinity. Give a simple geometric argument to show that the integral of each hn must be 1.
- Repeat Step 6 with the sequence
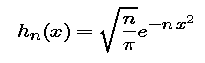
This time use your computer algebra system to verify that each function in the sequence has integral 1.