The One-Dimensional Heat Equation

Part 3: An Initial Condition Not Compatible with the Boundary Conditions

Now we consider a problem where the initial temperature distribution is not compatible with the boundary conditions. In the example we consider, the initial temperature distribution does not have values of 0 at the end points, but the boundary conditions remain 0 at the end points.

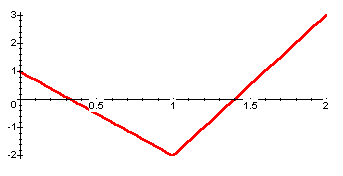
The mismatch between the initial condition and the boundary conditions puts stress on our model for the initial time steps. In our model, the temperature at the end points will immediately jump to the boundary values; the model does not describe this transition well. Also, the effects of the Fourier approximation are apparent for small time.

1. Calculate the first 15 coefficients for the Fourier sine expansion of g and compare the graphs of the approximations to the graph of g itself. Notice where the approximations differ most from g and how they differ.

2. Now study the approximate time snapshots of the solution to the initial/boundary value problem. Pay attention to the behavior for small time t. How are the differences between the initial condition and the Fourier sine approximations reflected in the time evolution?