|
|
|
|
|
|
In this module we will use the Residue Theorem of complex analysis to obtain inverse Laplace transforms of functions F(s). Our first step will be to identify a transform pair f(t) and F(s) for illustration in the development.
Use your computer algebra system to verify that the Laplace transform F of f is given by
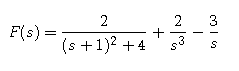
We begin our search for an inversion procedure for the Laplace transform by looking at the inversion process that we know for the Fourier transform. Suppose g is an absolutely integrable function on the real line. Then we know that
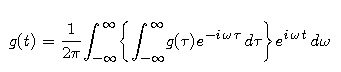
Now our test function f grows like t2 as t approaches infinity. So for any positive number a, the function g defined by
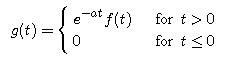
is absolutely integrable. (Here we use the fact that, for positive values of t, the negative exponential "kills" the polynomial growth -- and g is zero for negative values of t.) Thus, for positive t,
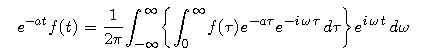
Now multiply both sides of this equation by eat to obtain
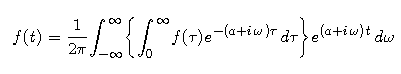
Compare the inside integral in this representation of f to the definition of F as the Laplace transform of f:
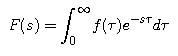
If we extend the definition of F to allow complex values for the independent variable, the inside integral in our representation for f is just F(a + i omega), and our formula for f becomes
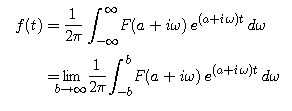
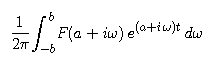
converge very slowly. To see why, set a = 1 and t = 1 and plot
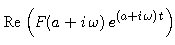
as a function of omega.
|
|
|
| modules at math.duke.edu | Copyright CCP and the author(s), 1999-2001 |