Go to CCP Homepage Go to Materials Page Go to Engineering Mathematics Materials  Go to Table of Contents 
Go Back One Page 

The Inverse Laplace Transform

Part 3: The Inversion Theorem

The calculations in Parts 1 and 2 have illustrated the following theorem.

Theorem. Suppose F is a function such that

  1. F(z) is differentiable for all z except for a finite numbers of poles at z1, z2, ..., zn.

  2. There exist numbers M and R such that |z F(z)| is bounded by M for all z with |z| greater than R.

For nonnegative t, define

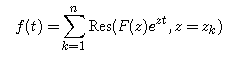
Definition of f

Then F is the Laplace transform of f.

  1. For the function F1 defined by

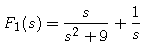
    use the theorem to find the inverse Laplace transform f. Use your computer algebra system's inverse Laplace transform routine to check the calculation.

  2. Repeat step 1 for the function F2 defined by

  3. Repeat step 1 for the function F3 defined by

 

Go to CCP Homepage Go to Materials Page Go to Engineering Mathematics Materials  Go to Table of Contents 
Go Back One Page 

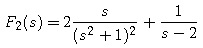
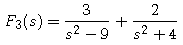
modules at math.duke.edu Copyright CCP and the author(s), 1999-2001