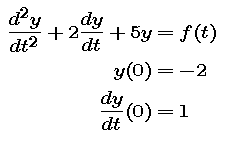Experiments with the Laplace Transform

Part 2. An ordinary differential equation problem

In this part, we will use the Laplace transform to describe the solution to the following initial value problem:

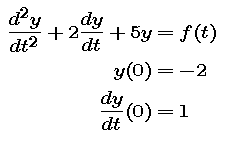
where the function f is the impulse function with the graph shown below.

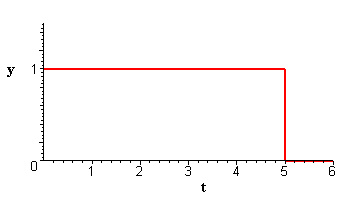
Graph of f

1. Calculate the Laplace transform F(s) of f(t).

2. Let y(t) be the solution of the initial value problem, and let Y(s) be the Laplace transform of the solution. Explain why Y(s) must satisfy
   

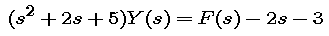
   Use your computer algebra system to find the inverse Laplace transform y(t) of Y(s).

3. Graph the function y(t).

4. Check that y(t) satisfies the two initial conditions.