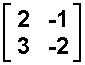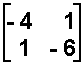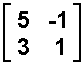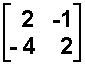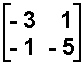Trajectories
of Linear Systems
Part 1: Real Eigenvalues
In this module we study
a number of systems of differential equations of the form
| x1' = a11
x1 + a12 x2 |
| x2' = a21
x1 + a22 x2 |
or, in matrix-vector notation,
X'
= AX,
where A is the matrix
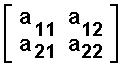 .
.
In your worksheet you will
find instructions for
- computing the eigenvalues
and eigenvectors of the matrix A, and
- drawing trajectories on
a direction field for the system.
For each of the following
systems (specified by the matrix A):
- Record the eigenvalues
and eigenvectors.
- Draw enough trajectories
to get a comprehensive view of the phase portrait of the system. (You will
have to add sets of initial conditions to those given.)
- Explain what features of
the phase portrait correspond to values of the eigenvalues and directions
determined by the eigenvectors.
- A =
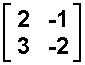
- A =
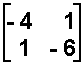
- A =
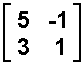
- A =
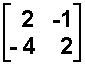
- A =
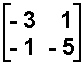
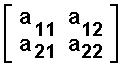 .
.