Complex Transcendental Functions

Part 1: The exponential function

We begin by examining the most fundamental of all transcendental functions -- the exponential function.

1. We define the exponential function as the sum of its power series
   

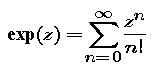
   Look at the simultaneous conformal plots of the exponential function and the nth polynomial approximation P_n, where P_n is just the nth partial sum of the defining series. How large must n be for a good approximation?

   The given plot is over a square with lower left corner at -2 - 2i and upper right corner at 2 + 2i. Repeat the exploration for a square with lower left corner at -4 - 4i and upper right corner at 4 + 4i. Now how large must n be for a good approximation? The series expansion of exp(z) is a Taylor series based at z₀ = 0. Explain why n must be larger in the second case.

2. Now look at the conformal plot of exp(z) by itself over the square with lower left corner -d - di and upper right corner d + di. Increase d from 0.5 to 3.5 in steps of 0.5. Describe the shapes of the images of vertical line segments under the exponential map. Now describe the shapes of the images of horizontal line segments under the exponential map.

3. Next consider the graph of the magnitude of the exponential function. Rotate the graph until you have a viewing aspect that appeals to you. Add coordinate axes. Relate the picture that you see here to the shapes of the images of horizontal and vertical lines from the conformal plot.

4. Now lets look at the real and imaginary parts of the exponential function. We'll consider each as a function of the two real variables x and y, where the complex variable z is written
   z = x + i y.

   Display both graphs. In what ways are they similar? In what ways are they different? (You may find it helpful to impose axes on the graph.)

5. The complex exponential function satisfies the basic law of exponents
   exp(z₁ + z₂) = exp(z₁) exp(z₂).

   This is not easy to show from the series definition we have given. For the moment, we will merely illustrate this property. Pick a specific pair of complex numbers z₁ and z₂. Calculate

   

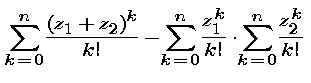
   for n = 10, 20, and 30. Repeat this for two more pairs of complex numbers z₁ and z₂. Summarize your calculations, and describe what the results of your calculations actually show.

6. Use the basic exponential property of the complex exponential function
   

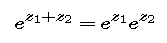
   to show that if the complex number z has real part x and imaginary part y, then

   exp(x + iy) = exp(x) [cos(y) + i sin(y)].

   Show how this property explains the conclusions you obtained in Step 2.

7. Derive the formula