|
|
|
|
|
|
Thus far, working from a single example, we have extracted two general principles:
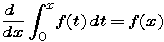
and
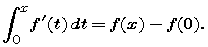
In this part and the next, we explore the same concepts in the context of two additional examples. Our first example was one for which you might or might not have recognized the symbolic formulas for the various functions involved. In this part you will certainly recognize all the formulas that appear. In the next part, you will almost certainly not recognize the antiderivative formula produced by your computer algebra system. The point of these examples is that it doesn't matter whether the formulas are familiar or even whether they exist -- our first general principle is a true statement about continuous functions in general, and the second is true about differentiable functions in general.
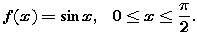
Graph this function.
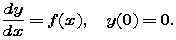
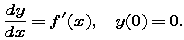
|
|
|
| modules at math.duke.edu | Copyright CCP and the author(s), 1999 |