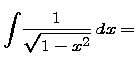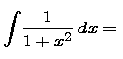Inverse Functions
Part 5: Summary
- Complete each of the following formulas:
Note that the last two of these are indefinite integrals, not definite integrals. All four of these are basic facts that you should know without having to look them up.
- Given a function definition, y = f(x), describe in words how you would find the derivative of the inverse function f-1. Carry out this process for y = ex. The result should be a formula (one you know already) for the derivative of the natural logarithm function.
- Suppose you know a formula for the derivative g'(x) of an unknown function g, and you also know that g(0) = 0. Explain how to write a formula for g(x) using definite integrals. Illustrate this process by finding a formula for the function g(x) = ln(x + 1), starting from the fact that g'(x) = 1/(x + 1).
|
CCP Home |
Materials | Integral Calculus | Module Contents | Back |