|
|
|
|
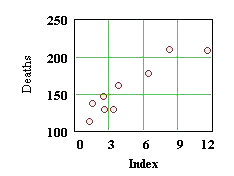
The Hanford Atomic Energy Plant in Washington has been a plutonium production facility since World War II, and some of the wastes have been stored in pits in the same area. Radioactive waste has been seeping into the Columbia River since that time, and eight Oregon counties and the city of Portland have been exposed to radioactive contamination. The table below lists the number of cancer deaths per 100,000 residents for Portland and these counties. It also lists an index of exposure that measures the proximity of the residents to the contamination. The index assumes that exposure is directly proportional to river frontage and inversely proportional both to the distance from Hanford and to the square of the county's (or city's) average depth away from the river. The accompanying figure is a scatter plot of the deaths vs. index data.
|
|
Even though the data points do not lie on a straight line, they exhibit a definitely linear trend. The problem of least squares is to find the line that "best fits" the data. Our next figure shows a candidate for such a line, along with vertical line segments indicating the deviations or residuals, that is, the (directed) distances from the data points to the corresponding points on the model line. For reasons we will see shortly, our criterion for best fit is that the choice of line should minimize the sum of the squares of the residuals -- hence the name "least squares." The best fitting line is called the least squares line or the regression line.
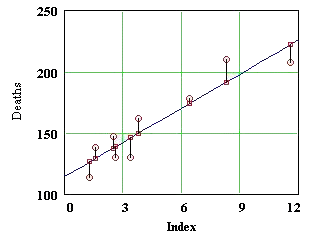
Remark about notation: Throughout this module, incontrast to our conventions elsewhere in the linear algebra materials, we will maintain a distinction between vectors and scalars by boldfacing vector names but not boldfacing scalars.
where m and b are real numbers.
|
|