|
|
|
|
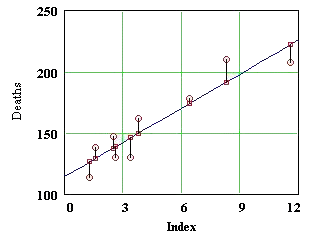
Describe in your own words the problem of finding the best fitting line for this data. In what vector space can this be formulated as a linear algebra problem? What linear algebra problem is equivalent to finding the coefficients of the least squares line?
|
|