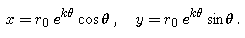The Equiangular Spiral
(Alternate Version)
Part 4: Why "Equiangular"?
The name "equiangular spiral" suggests that some collection of angles related to this curve are all the same -- equal -- constant. In this part of the module, we will explore first what's constant about this type of spiral. Then we will look at what that has to do with angles.
- You should have found in Parts 2 and 3 that the nautilus seashell curve has a polar formula of the form
where r0 is the value of r at theta = 0 and k is a constant that incorporates both a multiple of pi and a growth constant. (Your formula may not look exactly like this, but it should be equivalent.) Explain why the ratio
is constant. That is, the rate of growth of r is proportional to r itself.
Now we consider how that constant
proportional growth rate is related to a constant angle. In the following figure,
we show a segment of polar curve in red, along with three angles associated with
a given point on the curve:
- the polar angle theta to
the point,
- the angle alpha from
horizontal to the tangent to the curve, and
- the angle beta between
the tangent and the radius through the point.
We see from the figure that alpha = theta + beta, so beta = alpha -
theta. Now use a formula from trigonometry to relate tan(beta) to the
tangents of the other two angles:
The tangents in this formula are easy to relate to the (x,y) coordinates
of the point on the curve:
- We know from the polar to cartesian change-of-coordinate formulas (which you used in Part 3) that
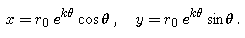
Find derivatives of x and y with respect to theta, and
then combine the results to find dy/dx in terms of theta.
You may want to use your helper application for this.
- In the formula for tan(beta), substitute the expression from the preceding step for tan(alpha), and substitute sin(theta)/cos(theta) for tan(theta). Simplify the resulting expression as much as possible. You definitely want assistance from your helper application here -- but you may have to help it see what steps to take.
- Explain why the angle beta is constant -- that is, why beta is the same for every point on the spiral. That's the equiangle!
- Explain the relationship between beta and the constant ratio of growth rate of r to r itself.
