|
|
|
|
| Theorem: Let C
be a piecewise smooth, simple, closed curve in the plane, and let D
be the region bounded by the curve C. The curve C is traced
out in such a way that the region D is always "to the left". If
the functions P(x,y) and Q(x,y)
have continuous partial derivatives on an open region of the plane that
contains D then: |
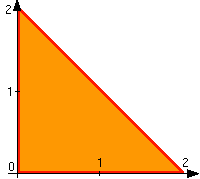 Set
up and evaluate the line integral
Set
up and evaluate the line integral
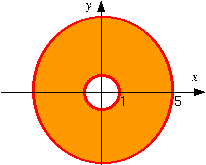 Set
up and evaluate the iterated integral
Set
up and evaluate the iterated integral
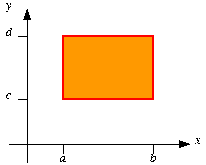 Next
we examine why the theorem works in a very special case, namely, when
the region is the rectangle D shown at the right, and the curve is the
boundary of the rectangle, R, traced out in a counter-clockwise direction.
Next
we examine why the theorem works in a very special case, namely, when
the region is the rectangle D shown at the right, and the curve is the
boundary of the rectangle, R, traced out in a counter-clockwise direction.
|
|
| modules at math.duke.edu | Copyright CCP and the author(s), 1999 |