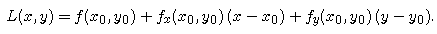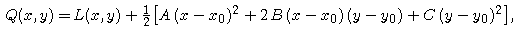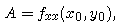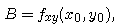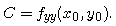Contour Plots and Critical Points
Part 2: First- and Second-Degree Taylor Approximations
At each point (x0, y0) in the domain of f, we can construct a first-degree Taylor approximation -- i.e., a best-fitting linear function L(x,y) -- by the formula
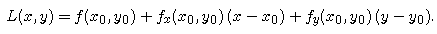
We see from the formula that f and L have the same value at (x0, y0), as do the first partial derivatives fx and Lx, fy and Ly. The graph of L is the tangent plane to the graph of f at (x0, y0).
Similarly, we can construct the second-degree Taylor approximation at (x0, y0) -- a best-fitting quadratic function Q(x,y) -- by
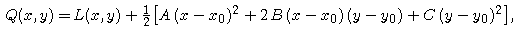
where the coefficients A, B, and C are given by
At (x0, y0), Q shares with f the function value and all values of first and second partial derivatives.
- Use your helper application to calculate the three second partial derivatives. (The expressions for these derivatives are quite complex, so you may not want to display them.)
- Choose an arbitrary point (x0, y0) in the domain [-3,3] x [-5,5]. We will use contour plots to examine the first- and second-degree Taylor approximations of f at (x0, y0).
- Define the first-degree Taylor approximation L to f near (x0, y0), and display the contour plots of both f and L together over a square
[x0 - delta, x0 + delta] x [y0 - delta, y0 + delta].
Start with delta = 0.5, and reduce to 0.1. Describe the extent to which the contours for L resemble the contours for f.
- Now define the second-degree Taylor approximation Q at (x0, y0), and repeat the experiment with the contours for f, L, and Q displayed simultaneously. Compare the extents to which the contours for L and the contours for Q each resemble the contours for f.
- Repeat the experiment -- that is, steps 2, 3, and 4 -- with a different point (x0, y0).