Distributions of Data, part 2

Distributions of Data

Part 2: Distribution and Density Functions

In this part we extend our discussion from failure data for light bulbs to models for a general class of data distributions. In our first example, the failure time of a light bulb could be any value in the interval from zero to infinity. Data such as this -- that can take on any real value in some given interval -- is said to be continuously distributed. In contrast, the outcome of a roll of a die, will always be an integer from 1 to 6; it could never be 1.3 or pi or any other non-integer value between 1 and 6. Such data is said to be discrete. From now on we will concentrate on models for continuously distributed data.

In Part 1, the key functions in our analysis of the light bulb data were data were

F(t) = 1 - e^- rt

and its derivative,

f(t) = r e^- rt.

For a general continuous distribution, the distribution function F(t) describes the probability that a randomly selected data item will have a value less than t. (For light bulbs, "value" meant "lifetime.") Thus, the probability of a data value lying between t = a and t = b is F(b) - F(a). As we did with the light bulb data, we define the probability density function f(t) to be the derivative of the distribution function. So by the Fundamental Theorem of Calculus, we also have that the probability of a data value lying between t = a and t = b is

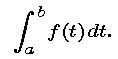
Our goal in modeling the distribution of given set of data is to find either an appropriate distribution function F or a an probability density function f. If F(t) is known, we find f(t) by differentiation. On the other hand, if f(t) is known, we find F(t) as a particular antiderivative of f(t), the one that has value 0 at the left end of the domain. Thus, a probability distribution can be specified by either its distribution function or its probability density function.

Arguing just as we did in Part 1, we define the expected value (also called average value) of a large data set distributed with density function f to be

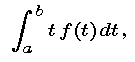
where the interval is selected to include all the possible outcomes. For example, to find the expected lifetime of light bulbs, the appropriate interval was from zero to infinity.

Different classes of data have different types of distributions and correspondingly different distribution and density functions. The distribution function F(t) = 1 - e^- rt is called an exponential distribution, and its derivative f(t) = re^- rt is called an exponential density. This model is the starting point for the study of reliability theory, which is useful for describing, among other things, failure times for electrical and electronic components such as chips in computers, batteries in toy rabbits, and bug zappers in backyards.

In this part we study two more types of distributions and their density functions. The first of these is the Cauchy distribution (pronounced ko-SHEE), which may be defined by the Cauchy probability density function:

Graph the Cauchy probability density function f.
Describe what the graph of the Cauchy probability density function says about the distribution of data values in a set modeled by this density function.
Show that the integral of f over its entire domain is 1.
Explain why, for any probability density function f, the integral of f over its entire domain must be 1.
Find a formula for the Cauchy distribution function F.
Evaluate
Explain why any continuous distribution function F must be an increasing function that approaches 0 at the left end of its domain and 1 at the right end.

We turn now to an example of a probability distribution that is much simpler than either the exponential or the Cauchy distribution. In fact, this example is so simple it is child's play.

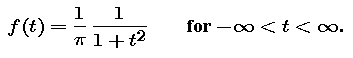
Suppose you have a spinner from a board game that randomly picks a value between 0 and 4, and you further subdivide the spinner into tenths of units. Thus you can decide whether the result of a spin is, say, greater than 2.3 and less than 3.6. We assume that this is a fair spinner -- for example, the result of a spin is as likely to give a value greater than 2 as a value less than 2. More generally, given two intervals of equal length, the probability of landing in one is the same as that for landing in the other. We suppose that we have a data set that consists of the numerical results from a large number of spins.

Explain why, for the spinner data just described, a reasonable density function is

f(t) = 1/4
for t greater than or equal to 0 and less than or equal to 4.

modules at math.duke.edu