|
|
|
|
|
|
Part 1: Background
Information:
The Law of Radioactive Change
and Disposal of Nuclear Wastes
Suppose we have a radioactive decay process of the general form
A --> products
This means that each atom of the radioactive substance A breaks down into a collection of smaller atoms and/or subatomic particles. Phenomena as diverse as dating ancient artifacts and assessing the dangers of nuclear wastes depend on knowing the rate of decay for such reactions.
Here are two examples of specific radioactive decay processes:
(a) (b)
In both cases, the notation
For more details on radioactive
decay processes, click here.
To return to this page from pages outside the CCP site, use your browser's
Back button. In 1903, Rutherford and
Soddy, in a paper entitled Radioactive Change, proposed the law
of radioactive change. They observed, in every case they investigated,
that the rate of decay of radioactive matter was proportional to
the amount present. If we write (as chemists do) [A] for the concentration
of the substance A, then the law of radioactive change becomes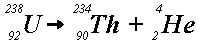
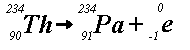
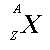 means
X is the chemical symbol for the element, A is the number
of nucleons (protons and neutrons), and Z is the number of protons.
Example (a) indicates that uranium-238 releases an alpha particle (i.e.,
a helium nucleus) to produce thorium-234. This is called alpha-decay.
Example (b) shows that thorium-234 releases a beta particle (i.e., an electron)
to produce protactinium-234. This is called beta-decay. Unstable
nuclides, such as uranium-238, start series of disintegrations that continue
until a stable nucleus results. Mass is lost in both alpha and beta decay
processes. This mass is converted into energy: radiation.
means
X is the chemical symbol for the element, A is the number
of nucleons (protons and neutrons), and Z is the number of protons.
Example (a) indicates that uranium-238 releases an alpha particle (i.e.,
a helium nucleus) to produce thorium-234. This is called alpha-decay.
Example (b) shows that thorium-234 releases a beta particle (i.e., an electron)
to produce protactinium-234. This is called beta-decay. Unstable
nuclides, such as uranium-238, start series of disintegrations that continue
until a stable nucleus results. Mass is lost in both alpha and beta decay
processes. This mass is converted into energy: radiation.
rate of change of [A] = -k [A].
The value of k is called the decay constant for A.
This law can be justified in the following way: For any fixed time interval, there is a certain probability (a number r between 0 and 1) that each atom of the radioactive substance will disintegrate. Thus, during this time interval, we should expect that the number of atoms that actually do disintegrate is r times the number present at the start of the interval. That's equivalent to saying that the rate of change of [A] is proportional to the amount present.
The functions that have rate of change proportional to the amount present are called exponential functions, and they have the form
y = y0bt
for some base b, where y0 is the starting amount. Thus, we would expect that a concentration function for a radioactive substance has the form
[A](t) = [A]0bt
where b is a number between 0 and 1 (in order to have decay rather than growth), and [A]0 is the starting concentration.
There are several quantitative aspects of radioactivity that are important for managing nuclear waste materials, including how much radioactivity a given substance emits, how concentrated the substance is in its surrounding medium, how dangerous its emissions are to human and other biological populations, and how long the substance goes on being radioactive. In this module we will address only the last of these issues, the time that a given substance remains dangerous.
There is a simple -- and delicious -- experiment you can carry out with a supply of M&M's to demonstrate the concept of half-life. Click here for the details.
For purposes of studying danger time durations, it is very important to know the half-lives of the radioactive materials invovled. Some nuclides decay to stable substances sufficiently fast (half-lives ranging from fractions of a second to a matter of days) that they are not a serious threat to the environment. On the other hand, some of the isotopes of plutonium have half-lives of many millions of years. And we have vast quantities of highly radioactive plutonium wastes from both weapon production and nuclear power generation.
Here are some sources for reading about the environmental impact of nuclear waste management:
|
|
|