Titration Project, Part 3

Titration

Part 3: Project

3.1. The Problem

You are a chemist working for an independent laboratory. You are leading a big project in which your team is performing quality control tests on several different acid products from several different manufacturers. With deadlines fast approaching, you've been forced to place your team under a strict schedule. But, somewhere in the rush, samples from 5 of the different products have gotten mislabeled, and now you and your team have no idea which sample is from which acid product. You know that each sample is one of five different weak acid solutions of unknown concentration. You don't have time to contact the manufacturers and have them send another set of samples. (Besides, that would be embarrassing!) What are you going to do?

Listed below are the five weak acids contained in the mislabeled solutions, along with their dissociation constants:

TABLE 3

weak acid	dissociation constant, K_a
hypochlorous acid	3.0 x 10^-8
potassium hydrogen phthalate	3.91 x 10^-6
acetic acid	1.75 x 10^-5
formic acid	1.77 x 10^-4
salicylic acid	1.05 x 10^-3

2. The Solution

You decide to perform acid-base titrations on the five unidentified acid solutions. (The concentrations of these solutions are unknown as well.) The data collected from one of these titrations are given in the table below.

Titration of 0.10 L of solution containing unknown concentration of an unknown acid with 0.09141 M NaOH (base)

v (L of base added)	pH of solution
0.00	4.54
.00101	4.55
.00220	4.61
.00329	4.70
.00419	4.72
.00517	4.79
.00623	4.81
.00740	4.88
.00858	4.90
.00963	4.97
.01074	5.00
.01150	5.02
.01290	5.04
.01399	5.11
.01510	5.15
.01615	5.20
.01730	5.22
.01849	5.26
.01978	5.30
.02083	5.33
.02197	5.38
.02285	5.40
.02389	5.42
.02502	5.49
.02611	5.50
.02721	5.54
.02809	5.60
.02929	5.63
.03051	5.69
.03150	5.75
.03270	5.80
.03365	5.89
.03483	5.95
.03573	6.02
.03689	6.15
.03711	6.21

v (L of base added)	pH of solution
.03734	6.22
.03759	6.25
.03789	6.29
.03809	6.34
.03835	6.39
.03861	6.48
.03890	6.53
.03914	6.65
.03935	6.71
.03951	6.80
.03975	6.98
.04000	7.30
.04021	8.60
.04030	9.12
.04053	9.43
.04079	9.64
.04091	9.71
.04111	9.80
.04130	9.88
.04159	9.96
.04180	10.00
.04210	10.06
.04229	10.10
.04251	10.15
.04275	10.20
.04300	10.21
.04401	10.29
.04510	10.38
.04625	10.43
.04733	10.49
.04839	10.50
.04949	10.52
.05069	10.59
.05189	10.60
.05289	10.61
.05400	10.62

(a) Identifying the Weak Acid

Recall that the equivalence point of any acid-base titration occurs when enough base has been added so that vc = a₀ A₀ [i.e., # moles OH^- (base) = # moles HA (acid)]. If v_equiv = volume of base at the equivalence point, then when v = v_equiv/2 the titration is said to be at half-equivalence point. So, at half-equivalence point, vc = a₀A₀/2, and therefore, referring to Table 1 in the Preliminaries, we can see that, at half-equivalence point,

[HA] = [A^-].

If this is the case, what can be said about the relationship between the dissociation constant K_a and H^- at half-equivalence point? Complete the following statement: Using the definition of K_a given in equation (2) of the Preliminaries, we find that, at half-equivalence point,

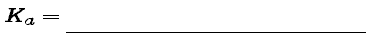(7)

(i) Using your Computer Algebra System, plot the titration data provided, and estimate v_equiv by locating the point in the titration graph of fastest increase. To help find this point, you may want to create and plot a data list of numerical first derivative values.

(ii) As mentioned above, half-equivalence point occurs at v = v_equiv/2. Use your estimate for v_equiv from part (i) to estimate the value of v at half-equivalence point. What was the pH of your solution at half-equivalence point?

pH of solution at half-equivalence point:

(iii) Use the pH value from part (ii) and the relationship described in equation (7) to determine the dissociation constant K_a for this unknown weak acid. (Recall that pH = -log[H⁺].)

(iv) The dissociation constant of an acid characterizes that acid. In other words, one can identify an acid by determining its dissociation constant. Identify the unknown weak acid in this solution by consulting Table 3, which lists the dissociation constants for the five weak acids contained in the mislabeled solutions.

The unknown acid in this mislabeled solution is:

(b) Determining the Initial Concentration

Now that you have identified the acid in this mislabeled solution, you are ready to perform the quality control test on it as originally planned. The manufacturer claims that the concentration of acid in this particular product is 0.05 M. Your job is to determine independently the concentration of acid in your sample in order to test the validity of the manufacturer's claim.

(i) You will make use of the titration data for this mislabeled solution once again. The titration was of 0.10 L of acid solution with 0.09141 M NaOH. Using your Computer Algebra System, define a function to be the titration modeling function H(v) that gives the pH of the solution corresponding to v liters of base added. Choose appropriate values for the parameters a₀, c, and K_a. Use the value for K_a from part (a)-(iii). You will want to be able to try different values for the fourth parameter, A_0, the initial concentration of acid.

(ii) Determine the concentration of acid in this mislabeled solution by finding the value of the parameter A₀ for which the model H(v) best fits the titration data. Since H(v) is not a basic function, there are no quick and easy methods for fitting it to data. One can do a sufficient job, however, by plotting the modeling function H(v) for a particular value of A₀ together with the titration data, and then replotting the two graphs over and over again -- each time trying a different value for A₀ -- until the titration modeling function best fits the titration data. Go through this process and determine the concentration of acid in this mislabeled solution. We suggest that you begin with the value of A₀ claimed by the manufacturer: A₀ = 0.05 M. The desired graph for this value of A₀ is shown below. You will generate similar graphs, experimenting with values of A₀ to obtain the best fit.

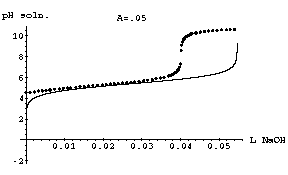
Important Note: Keep in mind as you are experimenting with values of A₀ what part of the modeling function H(v) should fit the data best. Recall that the two simplifying assumptions we made while building this model are both valid only when v is not near zero and less than the equivalence point. So, don't worry about fitting the model to the data near v=0 or for v > v_equiv, since the model is not valid in those regions.

Concentration of Acid in this mislabeled solution:

Now that you have determined the best value for A₀, you have a well-fitting model function H(v). One reason for modeling data is that it is often easier to analyze a continuous function than it is to analyze data. The section of a titration graph where the pH increases slowly is called the buffer region. This should be the region where your modeling function H(v) best fits the titration data, so let's analyze your function in this region.

(i) Using your function H(v) (with all parameters now determined), find the value of v for which H(v) increases the slowest. Be as accurate as possible. You will probably want to use graphs of the first and second derivatives of H(v) to determine this value. Explain how these two graphs can help you find the point of slowest growth for H(v) -- which should be the half-equivalence point. Double this value to obtain your model's prediction for the value of v at the equivalence point, v = v_equiv. You also estimated v_equiv from your data in part (a)-(i). How close did the estimate come to the value for v_equiv predicted by your model?

Value for v_equiv predicted by model =

(ii) Use the value for half-equivalence predicted by your model to determine (once again) the dissociation constant K_a of this acid. [Keep in mind the relationship you stated in equation (7).]

You should have achieved the exact value for K_a listed in Table 3. If you think you haven't, then check again! It might be that your value is simply expressed with a different power of 10.