Experiments with Fourier Series

Part 3: Fourier Approximations to a Saw-Tooth Wave

Now we consider a function f that is not continuous everywhere:

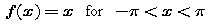
where f is extended to be 2 pi-periodic. The extension makes the function discontinuous at integer multiples of pi.

1. Give a graphical explanation of why a₀ = 0.
   
   
2. Calculate the other coefficients a_k. How could we have known in advance what these coefficients would be?
   
   
3. Calculate the coefficients b_k. Write down the simplified form of these coefficients you obtain by using the fact that k is an integer.
   
   
4. Describe the values of cos(pi k) for k = 1, 2, ... .
   
   
5. Compare the Fourier approximations with the function f. What is happening at the points of discontinuity? What is the value of each of the approximations at these points?

modules at math.duke.edu