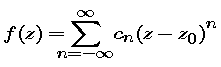Go to CCP Homepage Go to Materials Page Go to Engineering Mathematics Materials Go to Table of Contents
Go Back One Page

Isolated Singularities and Series Expansions

Part 5: Summary

If the function f has an isolated singularity at z0, then it has a Laurent series expansion in some punctured disk centered at z0:

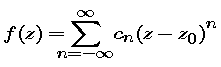
  1. How can you tell from a Laurent series whether an isolated singularity is a removable singularity, a pole, or an essential singularity?

  2. How can you tell the order of a pole from a Laurent expansion about the pole?

  3. How do you describe the behavior of |f(z)| near a removable singularity? near a pole? near an essential singularity?

  4. At least two of the functions studied in this module have essential singularities. What was your strategy for finding Laurent series expansions around each of these essential singularities?

  5. How can you find the residue of f at z0 from the Laurent series for f at z0?

Go to CCP Homepage Go to Materials Page Go to Engineering Mathematics Materials Go to Table of Contents
Go Back One Page

modules at math.duke.edu Copyright CCP and the author(s), 1998-2001