Population Growth Models
Part 4.3: Inflection Points and Concavity
Now we consider non-equilibrium solutions for the logistic equation. Some of the solutions have an inflection point -- and so change concavity -- and some do not.
- Which solutions of
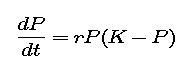
appear to have an inflection point? Express your answer in terms of starting values P(0). [For your convenience, the interactive figure from Part 2 is repeated here. Recall that the vertical coordinate of the point at which you click is P(0) and the horizontal coordinate is ignored.]
- Use your observations in Step 1 to determine how the value of P at the inflection point (when there is one) seems to be related to K.
- Starting with the differential equation, differentiate again to obtain a formula for d2P/dt2 in terms of P and dP/dt. For what values of P is the second derivative zero? Does this agree with your conclusion in Step 2?
- What is the significance of the inflection point in terms of the population growth rate?
