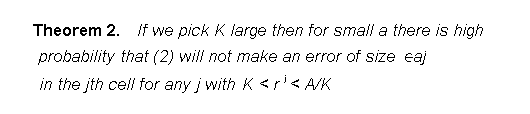
To state our result for small sizes we need to introduce p(t), the density of particles at time t when in a coalescing random walk when we start with all sites occupied, and let

be our approximation of the expected value of the number of clusters with sizes in [M,Mr). Using an asymptotic formula due to Bramson and Griffeath (1980) and a little calculus shows that the expected number of observations in the jth cell satisfies:


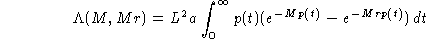
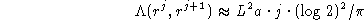
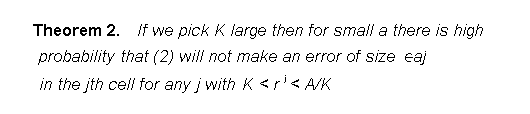
Recall sizes that are multiples of A are treated in Theorem 3. Small sizes have to be treated by special methods since our asymptotic formula for p(t) cannot be used.

The circles in the graph on page 2 give the number of observations predicted by this formula. This time the fit is poor. If, however, we use the formula in (1) directly the curve of squares results. Further, if we take the minimum of the square curve and the triangle curve then we have

(i) an accurate fit for the simulation data across the whole range

and (ii) a curve with a shape that resembles Hubbell's data.

Back to the home page