|
|
|
|
|
|
Although the air we breathe seems weightless, each of the gases that make up air has a certain weight associated with it. The fact is, the force of gravity on the mass of a column of air of unit cross-sectional area defines ``atmospheric pressure.'' It makes sense from a physical point of view that the measured atmospheric pressure should decrease as one moves to higher altitudes. Think of a tube of a certain cross-sectional area containing marbles. The marbles on the bottom of the stack would have the highest ``pressure'' exerted on them because all of the other marbles above would be pressing down on them with all of their combined weight. Marbles in the center of the stack have fewer marbles above pressing down on them, so the ``pressure'' they see would be considerably less.
Now, if we were to add up the weights of all the gas molecules pressing down on a certain unit area at say, 5 km above the earth's surface (a unit area in the middle of the container of marbles), our pressure measurement would be less than the same pressure measurement on the earth's surface. This is the reason that commercial airlines pressurize their passenger cabins and mountain climbers often carry oxygen tanks with them. The air at these higher altitudes is at lower atmospheric pressure or is ``thinner.'' This phenomenon in which pressure decreases with increasing altitude occurs in all fluids (liquids and gases) and is particularly pronounced when water is the fluid. Take the oceans, for example. On the ocean floor the water pressure can be enormous! This is why submarines and other deep sea diving vessels must have thick walls to prevent them from being crushed under tremendous water pressures.
Atmospheric chemists refer to the mathematical relationship describing this phenomenon as the barometric equation. The barometric equation states that the rate of change in pressure, P, relative to altitude, a, is proportional to the density, 
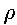, (mass per unit volume) of the fluid (in this case, air) where the proportionality constant is the negative of the acceleration due to gravity, g:
|
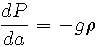
(1) |
The Ideal Gas Law provides information about the relationship among pressure, volume, molecular weight, number of moles of gas and temperature for a particular gas. The Ideal Gas Law is actually a composite of three different gas laws: Boyle's Law, Charles' Law and Avogadro's Law. All of these laws were discovered empirically, that is, they were formulated entirely from experimental data.
Boyle's Law states that pressure is inversely proportional to volume at a constant temperature and a constant amount of gas. Boyle's Law basically says that gases are compressible -- greater pressure results when a gas is compressed (i.e., when its volume is reduced.)
Charles' Law relates temperature and volume, and states that at constant pressure, the volume of a given amount of gas is proportional to its temperature. Charles' Law can be illustrated by considering a hot-air balloon. As the air in the balloon is heated, the volume occupied by the air in the balloon increases, thus lowering the effective density (lower weight of air per unit volume) of the air inside the balloon. The balloon will rise in the atmosphere until it encounters air of similar density outside the balloon.
Avogadro's Law relates the amount of gas to volume. Avogadro was the first to suggest that the volume of a gas is proportional to the number of gas molecules present at a given temperature and pressure. Pumping up a flat tire is an application of Avogadro's Law.
We can combine all three of these into the Ideal Gas Law, which states that
 |
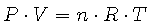(2) |
where
Notice that each of the three laws mentioned is a special case of the Ideal Gas Law.
If we divide the mass of gas, m (kg), by its molecular weight, M (kg/mole), we obtain the number of moles of gas. This expression can be substituted for n = m/M in Equation 2 to obtain
 |
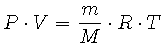Upon rearrangement we get
 |
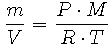Note that m/V is the definition of density and is denoted as 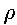. Since we are formulating an expression for the density of air, which is a mixture of several gases, we will use an average molecular weight of air, Mair, which we will calculate shortly. Mair is measured in kg/mole. So
 |
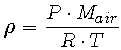(3) |
where 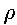is measured in units of .
Restate the barometric equation (1) by replacing the value of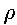
from (3):
 |
(4) |
We will assume for the purposes of this project that g, R, Mair, and T are constant relative to altitude. Solve the differential equation (Equation 4) to obtain an expression for P(a) describing pressure as a function of altitude. Let P0 = 1.013 x 105 kg / (m sec2) represent the initial pressure which we take to represent the pressure at the earth's surface (a = 0).
 |
(5) |
Let
 |
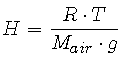and restate P(a) in terms of a, H and P0:
|
|
(6) |
Atmospheric chemists refer to the combined parameter H as the scale height. Recall that the pressure (and thus, density) of air decreases with increasing altitude. The scale height, H, can be thought of as the height the entire atmosphere would have if its density were constant at the sea level value throughout [1, pp. 213-215].
We can compute the scale height, H, by determining the values of each of its parameters. Mair can be calculated from the fractional composition and the molecular weight of each component in the air by taking a weighted average. The table below lists the significant chemical components of air along with their individual fractional amounts and molecular weights.
| element | fraction of air | M (kg/mole) |
| N2 | 0.78080 | .028013 |
| O2 | 0.20950 | .031999 |
| Ar | 0.00930 | .039948 |
| CO2 | 0.00034 | .044010 |
Calculate the molecular weight of air by taking a weighted average of the molecular weights of its chemical components:
 |
 |
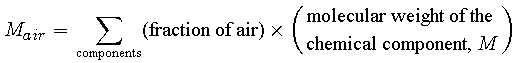(7) |
If we assume that near the earth's surface the global average air temperature is 285 K, the gas constant, R, is 8.3144 m2kg / (sec2 K Mole), and the acceleration of gravity, g, is 9.80 m / sec2, then from
|
|
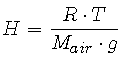we have
 |
(8) |
We can now re-express P(a) using Equations 6 and 8.
|
|
(9) |
Our work will require that we shift our focus from pressure as a function of altitude to concentration of oxygen as a function of altitude. To accomplish this recall from Equation 2 that pressure and concentration can be related to each other through the Ideal Gas Law:
 |
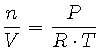(10) |
What would be the unit of measure for concentration, n/V?
Atmospheric chemists prefer to work in units of (molecules / m3), so the concentration quantity from the above equation should be multiplied by Avogadro's number, 6.022 x 1023 (molecules / mole). Additionally not every air molecule is an oxygen molecule, O2, so in order to obtain an expression for concentration of O2 we also need to multiply the concentration of air by the fractional abundance of O2 in the air, which is 0.2095.
 |
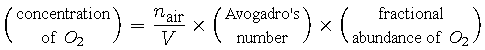(11) |
We can now express C(a) as the concentration of oxygen at a given altitude. Use Equations 9, 10 and 11 to write C(a) in terms of P0, R, T, and a:
 |
(12) |
Now let
 |
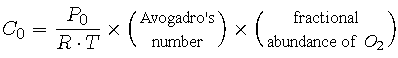and rewrite C(a) in terms of C0 and a:
|
|
(13) |
Use a computer algebra system to enter C(a) as a function of a with all of its parametric components defined. Enter the results of your computations in the space below. [Note: Your function C(a) should contain only one variable (a) and C0 should be a number!]
|
|
(14) |
where
 |
|
|
|
modules at math.duke.edu
Copyright CCP and the author(s), 1999
