|
|
|
|
|
|
Let us consider passing light of a single wavelength (of a certain energy) through a substance that tends to absorb light. It makes sense from a qualitative point of view that the intensity of the light (or photon flux) should diminish as the light travels through the substance. In essence, the more light-absorbing molecules with which the incident light comes into contact, the more the light intensity decreases.
There are two important parameters that determine how many light-absorbing molecules a given incident light will contact. The first is the concentration of the absorbing molecules. As the concentration increases, the light intensity will be attenuated by a greater amount. The second parameter is the length of the path the light takes through the absorbing medium. As the path length increases, the light will come into contact with more absorbing molecules, and thus the light intensity will diminish.
As an example of the importance of these two parameters when calculating light intensity, consider holding a penlight up to a glass of grape juice. You can imagine that if you increase the concentration of the juice (make it stronger), the juice will be more intensely colored and thus will attenuate light to a greater extent as it travels to the other side of the glass. Similarly, if you prepare the juice in a large pitcher rather than a glass, the light will have more difficulty going through to the other side, because the path length that the light must travel has been increased.
There is yet another term that greatly affects how light is absorbed by a
substance. In this project, the term is called the absorption cross section,
To formulate a differential equation that examines the change in photon flux relative to change in altitude, we use a form of Beer's Law, which states that the rate of change in photon flux relative to altitude is the product of the amount of photon flux present, the concentration of light absorbing species present at a particular altitude, and the ability of the absorbing species to absorb light of a certain wavelength. This is described by the differential equation
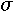 . This term
can be thought of as the ability of a particular molecule to absorb light of
a certain wavelength. To illustrate, let's return to the glass of grape juice.
The grape juice is not able to absorb all possible wavelengths of light to the
same extent. The molecules in the juice may be able to absorb wavelengths in
the range of 570 nm very well for example, but they may be unable to absorb
any other wavelength to any appreciable extent. For instance, since we see purple
light, grape juice must not be able to absorb purple light.
. This term
can be thought of as the ability of a particular molecule to absorb light of
a certain wavelength. To illustrate, let's return to the glass of grape juice.
The grape juice is not able to absorb all possible wavelengths of light to the
same extent. The molecules in the juice may be able to absorb wavelengths in
the range of 570 nm very well for example, but they may be unable to absorb
any other wavelength to any appreciable extent. For instance, since we see purple
light, grape juice must not be able to absorb purple light.
 |
(15) |
where
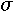 = absorption cross section of the absorbing species.
= absorption cross section of the absorbing species.
Beer's Law is usually expressed with a negative sign on the right side of the equation, but in our model the negative sign is dropped because of the referencing system for altitude and photon flux.
Recall that our model describes the photon flux (I) as a function of altitude (a) and assumes that the only absorber of light is the oxygen molecule, O2. We have chosen 240 NM as the wavelength of light for our model because it is in the ultraviolet range of light where oxygen absorbs most readily. The value for the absorption cross section of O2 at this wavelength is 1.0 x 10-28 m2. The photon flux from the sun at this wavelength, I0, is 7.61 x 1017 photons/(m2sec).
Combine Beer's Law with Equation 13, and use separation of variables to solve for I(a). Your initial condition for this IVP is that I(a) = I0 when 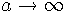 (top of the atmosphere).
(top of the atmosphere).
 |
(16) |
|
|
|
| modules at math.duke.edu | Copyright CCP and the author(s), 1999 |