Functions Defined by Integrals, Part 5

Functions Defined by Integrals

Part 5: The Fundamental Theorems

The following statement is called the First Fundamental Theorem of Calculus (FTC1): If f is any continuous function whose domain includes 0, then

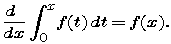
We established the truth of this statement in Part 1.

In Part 2 we showed that, if f is any differentiable function whose domain includes 0, then

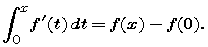
This statement is not quite the Second Fundamental Theorem, but we can easily derive the theorem from it.

First, suppose that h is any function whose derivative is the same as the derivative of f -- that is, h '(x) = f '(x). Show that

It follows from step 1 that

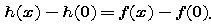
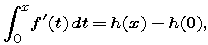
where h is any antiderivative of f '. There is nothing special in this formula about the names f ' and h. For example, we could state the same fact this way:

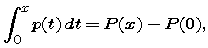
where p is a continuous function with 0 in its domain, and P is any antiderivative of p. This is the Second Fundamental Theorem of Calculus (FTC2) -- although it is usually stated in different notation.

Next we see that there is nothing special about 0 as the fixed "base" for definite integration to the variable upper limit in either FTC1 or FTC2.

Show that, if f is a continuous function, and a is a number in its domain, then

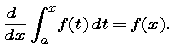
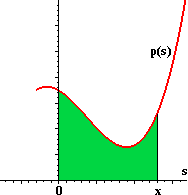
[Hint: Recall the argument that led to this formula, based on estimating a difference quotient for F(x). By the time we calculated a difference of values of F, there was no longer any mention of the left end point of integration. Thus, that left end point could have been any a and the answer would have been the same.]
Show that, if f is a continuous function on the interval [a,b], then

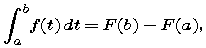
where F is any antiderivative of f.
[Hint: A strategy is suggested by the following figures:

The relevant integral is shown as the shaded area in the left figure. The right figure is the same except the horizontal scale has been shifted by setting s = t - a and x = b - a. Define the functions p and P by p(s) = f(s+a) and P(s) = F(s+a), respectively. Then show that P is an antiderivative of p (remember the Chain Rule). The desired result follows from FTC2 as stated before step 2.]

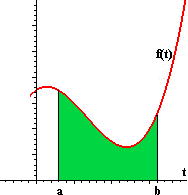
Steps 2 and 3 give the conventional statements of FTC1 and FTC2. Naming of the fundamental theorems is not universally agreed upon. In some textbooks they are numbered in the other order. Sometimes they are stated as a single Fundamental Theorem with parts 1 and 2, again with the order determined by the author.