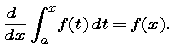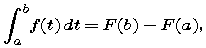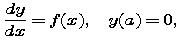Functions Defined by Integrals

Part 6: Summary

1. Interpret the definition of the function F(x) in terms of "sweeping out area" under the graph of f(x). Why does it make sense that the instantaneous rate F'(x) at which area is swept out is equal to f(x)?

2. Explain carefully, in your own words, the First Fundamental Theorem of Calculus: If f is a continuous function and a is a number in its domain, then
   

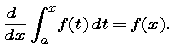
   [Note: "The derivative undoes the integral" is a true statement but not a careful explanation. In particular, describe precisely each of the elements of the left-hand side, and then say why you believe the equality to be true.]

3. Explain carefully, in your own words, the Second Fundamental Theorem of Calculus: If f is a continuous function on [a,b], then
   

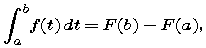
   where F is any antiderivative of f.

4. (optional) Explain carefully how a solution of the initial value problem
   

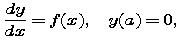
   where f is any continuous function, can always be constructed by using definite integration.