|
|
|
|
|
|
In this module, we will use your helper application's taylor command to construct Taylor polynomials, instead of asking you to construct the coefficients by differentiation. We begin by practicing the use of this command for the function f(x) defined by
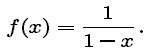
The constant polynomial P0 is just f(0), which is 1. However, when you ask your helper application for P0, it may respond 1 + O(x). This means that, for small values of x, the "error" [i.e., the difference between P0 and f(x)] is roughly proportional to x.
Similarly, when you ask for P1(x), you may see 1 + x + O(x2) instead of just 1 + x. This means that P1(x) actually is 1 + x, and (again, for small x) the error in approximating f(x) is roughly proportional to x2. To create a formula for a Taylor polynomial, you need to delete the "O" term. One way to do this is to highlight and copy all of the output formula except that term, and then paste wherever you need the formula.
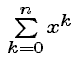
Explain the following formula:
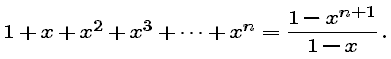
[Hint: Consider the expression you obtained in step 2 for Pn(x). Multiply by x to obtain an expression for x Pn(x), and subtract the result from the expression for Pn(x).]
The sum in step 3, in which each term is x times the preceding term, is called a geometric sum. The fact that we can also write this sum as the quotient of two (short) polynomials is very important. We will put it to use in the next part. Since a geometric sum with x as ratio of each term to the preceding one is also a polynomial in x, it is sometimes called a geometric polynomial.
|
|
|
| modules at math.duke.edu | Copyright CCP and the author(s), 1999 |