Taylor Polynomials II

Part 2: Convergence and Divergence

1. How do we know that the function

   

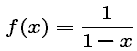
   is not a polynomial? State at least one property of this function that could not be a property of any polynomial.

2. Plot the function

   

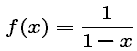
   together with its Taylor polynomials of degrees 0 through 5. For what values of  x  do the polynomials seem to be approximating  f(x) ?

3. We have the formula

   

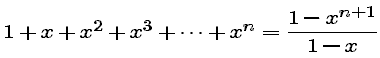
   for the n-th Taylor polynomial of  f(x), which makes it easy to define and plot Taylor polynomials of very high order. Plot  f(x)  together with its Taylor polynomials of degrees 20, 50, and 100. Also use some nearby odd values of n, such as 19, 49, 99. Do these calculations confirm your answer in step 2? If so, why? If not, how do you need to change your answer in step 2?

If  x  is a number for which

then the sequence of Taylor polynomials  P_n  is said to converge to  f  at  x. The set of all such numbers  x  is called the interval of convergence of the polynomial sequence. Outside the interval of convergence, the sequence is said to diverge.

4. What do you think is the interval of convergence for the sequence of Taylor polynomials of the function

   

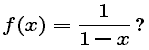
   Explain your answer.

5. Another way to write the formula in step 3 is



or



Thus, in order to have the sequence of polynomials converge to  f(x)  at a particular  x,  we must have



Explain why this limit formula is correct for  -1 < x < 1. Does this confirm your answer to step 4? Explain.

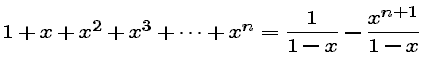
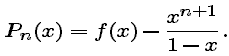
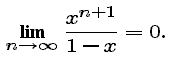
modules at math.duke.edu

Copyright CCP and the author(s), 2000