Taylor Polynomials II

Part 3: New Polynomials from Old

We can use our knowledge of the Taylor polynomials for  1/(1 - x)  to obtain the Taylor polynomials for other functions. For example, since

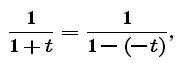
we can substitute  x = - t  in the formula

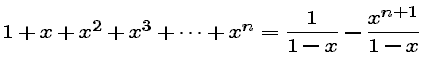
to find

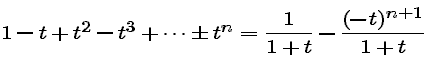
This suggests that the n-th Taylor polynomial for  1/(1 + t)  is

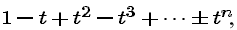
where the sign of  tⁿ  is + if  n  is even, - if  n  is odd.

1. Use your computer algebra system to confirm that this formula for Taylor polynomials of  1/(1 + t)  is correct.

2. What is the interval of convergence for the Taylor polynomials of  1/(1 + t) ? Explain how you know.

We know from the Fundamental Theorem of Calculus that

What happens if we integrate the Taylor polynomials for  1/(1 + t) ? We find

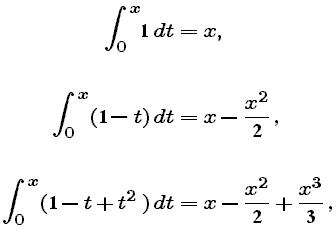
and, in general,

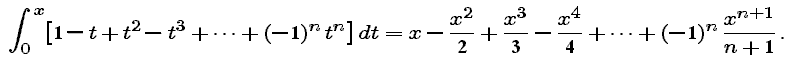
Are these the Taylor polynomials of  ln(1 + x) ? We explore that question in the next part.

modules at math.duke.edu

Copyright CCP and the author(s), 2000