|
|
|
|
|
|
|
|
In this module, as in the Difference Equations module, the principal objects of study will be sequences, that is lists of numbers. In this module, however, the sequences will be of the form
going on forever in
both directions. These are sometimes called doubly-infinite
sequences. (The sequences {y0,
y1, y2, y3,
...} that you studied before may be called singly-infinite
sequences.) Like a singly-infinite sequence, a doubly-infinite
sequence will be abbreviated as {yk}, this time
with the understanding that the index k takes on all
integer values --- positive, negative, and zero.
One place where this sort of sequence frequently appears is in engineering. Often there is a situation where you have some sort of continuous signal (for example, an electrical signal, a radio signal, a light signal, or a sound signal) that you want to measure. One way to do this is to sample the signal at regular intervals, for example, every second.
Let's be more concrete. Suppose we want to measure the following signal:
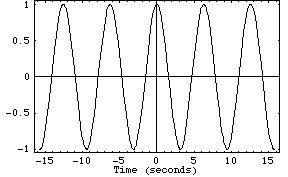
We can measure the strength of the signal at every quarter-second:
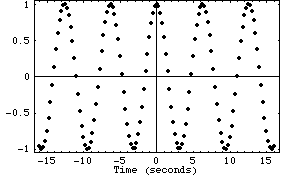
This gives us a pretty good picture of what the signal looks like. We can represent our samples as a sequence using the formula
where k represents the number of quarter-seconds from "time 0".
|
y-5 = 0.598472 |
|
y-4 = 0.909297 |
|
y-3 = 0.997495 |
|
y-2 = 0.841471 |
|
y-1 = 0.479426 |
|
y0 = 0 |
|
y1 = -0.479426 |
|
y2 = -0.841471 |
|
y3 = -0.997495 |
|
y4 = -0.909297 |
|
y5 = -0.598472 |
How might
you go about guessing a formula for the sequence? (Hint: you might
start by looking at a plot!) Make a guess for a formula and check
your answer.
|
y-5 = -2.59311 |
|
y-4 = -2.92405 |
|
y-3 = -0.566632 |
|
y-2 = 2.31175 |
|
y-1 = 3.06472 |
|
y0 = 1 |
|
y1 = -1.98411 |
|
y2 = -3.14404 |
|
y3 = -1.41335 |
|
y4 = 1.61676 |
|
y5 = 3.16044 |
Do you have enough information to guess a formula for the sequence? What makes you think you do or you don't?
which corresponds to sampling the signal below every second.
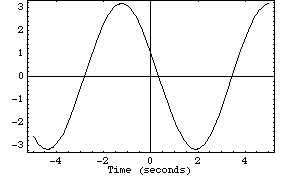
If instead
we sampled the same signal every tenth of a second, we would get
the sequence
Plot this formula from k = -50 to k = 50 . (This makes sense because 5 seconds is 50 tenths of a second.) Explain why sampling at a higher rate makes it easier to reconstruct the original signal.
|
|
|
|