Rotation Matrices
Part 1: Trigonometric Background
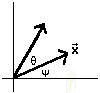
- Let (x,y) denote the terminal
point of the vector v in the plane. Suppose we rotate this vector
through an angle
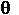 and let (xr,
yr) denote the new terminal point vr after
the rotation. Our first objective is to calculate the new coordinates
in terms of the old ones. If b = |v|, then x = b cos(
and let (xr,
yr) denote the new terminal point vr after
the rotation. Our first objective is to calculate the new coordinates
in terms of the old ones. If b = |v|, then x = b cos(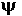 )
and y = b sin(
)
and y = b sin(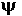 ). Similar formulas
give us xr and yr in terms of the angle
). Similar formulas
give us xr and yr in terms of the angle 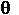 +
+
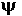 . Enter the formulas for xr
and yr, and use the expand function to rewrite these formulas
in terms of the angles
. Enter the formulas for xr
and yr, and use the expand function to rewrite these formulas
in terms of the angles 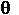 and
and 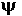 .
Then identify occurrences of x and y in these expressions, and rewrite
the formulas to give xr and yr in terms of x, y,
and
.
Then identify occurrences of x and y in these expressions, and rewrite
the formulas to give xr and yr in terms of x, y,
and 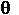 .
.
- Rewrite the transformation
(rotation through an angle
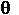 ) as
a matrix-vector equation, vr = Av. That is, give
the matrix A.
) as
a matrix-vector equation, vr = Av. That is, give
the matrix A.
modules at math.duke.edu

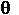 and let (xr,
yr) denote the new terminal point vr after
the rotation. Our first objective is to calculate the new coordinates
in terms of the old ones. If b = |v|, then x = b cos(
and let (xr,
yr) denote the new terminal point vr after
the rotation. Our first objective is to calculate the new coordinates
in terms of the old ones. If b = |v|, then x = b cos(