Go to CCP Homepage Go to Materials Page Go to Linear Algebra Materials Go to Table of Contents
Go Back One Page Go Forward One Page

Rotation Matrices

Part 2: Two-Dimensional Rotation Matrices

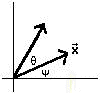
  1. Test your result from Part 1 by rotating the standard unit vector e1 in R2 through an angle of 60 degrees. First, use some scratch paper and trigonometry to see what the answer should be. Enter your hand-calculated image vector in the worksheet. Then let B be the 2 x 2 rotation matrix for an angle 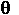of 60 degrees. (Enter B as a specific instance of A for the given angle. Recall that the built-in trigonometric functions expect angles in radians.) Check that your matrix B gives the same result as the hand calculation.

  2. Repeat the preceding step with the standard unit vector e2.

  3. Compute B6, B12, B18, and B24. Explain your results in terms of rotations. In particular how could you have predicted the particular matrices that the computer algebra system produced?

  4. Let K be the 2 x 2 rotation matrix for a rotation of 15 degrees. Compute B2, K4, K2B, KBK, and BK2. Compare the results and explain what you see.

  5. In general we know that matrix multiplication is not commutative; i.e., if B and K are both n x n matrices, then usually BK is not the same as KB. However, rotation matrices are a special case. Explain why, for any two 2-dimensional rotation matrices Q and R, it must follow that QR = RQ. Then use B and K from the preceding step to illustrate your argument.

  6. Explain why the product of any two 2 x 2 rotation matrices is another rotation matrix. Illustrate your argument with a specific example.

Go to CCP Homepage Go to Materials Page Go to Linear Algebra Materials Go to Table of Contents
Go Back One Page Go Forward One Page

modules at math.duke.edu