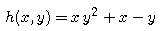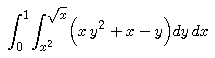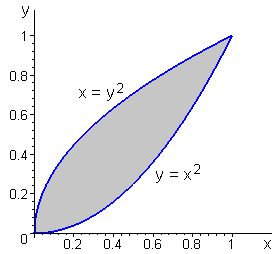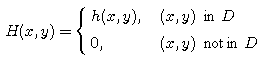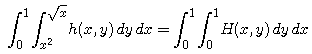Double Integrals I
Part 3: Double Integrals Over More General Regions
Now we study the integral of
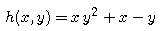
over the region bounded above by x = y2 and below by y = x2 (see the following figure), that is,
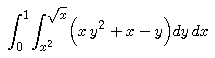
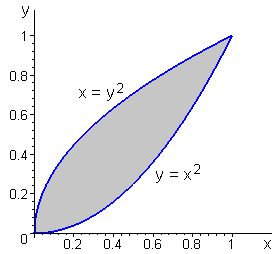
Let D denote the region between the graphs of x = y2 and y = x2, that is, the shaded region in the figure above. To calculate the integral of h(x,y) over D, we extend h to a function H defined by
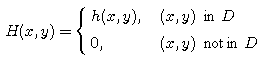
Then
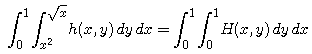
That is, we can evaluate the integral of h over D by instead integrating H over [0,1]x[0,1]. Since H is to be integrated over a rectangle, the method developed in Part 2 can be employed.
- Define the function h in your worksheet, and graph it over the rectangle [0,1]x[0,1]. If necessary, rotate the graph to get a good view of it.
- Define the extended function H in your worksheet, and graph it over the rectangle [0,1]x[0,1]. If necessary, rotate the graph to get a good view of it. Explain why integrating H over the entire rectangle gives the same result as integrating h over D.
- Use the extended function H and the definition of double integral to approximate the double integral of h over D with n = 10, 20, and 40. Record the results.
- For the same values of n, approximate the value of the integral of h over D using your improved method from Part 2, and record the results.
- This integral can be calculated exactly by hand. Do that, and compare the results with the approximations in the two preceding steps.