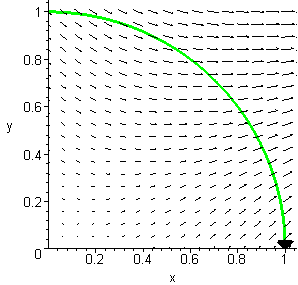
Vector Fields and
Line integrals
Part 4: Approximating the Work Done Along a Curved Path
In
Part 2 you calculated work done when a constant force acts on an object
that moves along a straight path. Using the applet in Part 3, you found
the work done when a non-constant force acts on an object along a curved
path. [A non-constant force
is one for which the direction or the length (or both) of the arrows changes from
point to point.] In this part
you will learn one way to calculate the work done when the force is not
constant and the path is not a straight line.
We can approximate a curved path
by a collection of straight lines. The figures below show a quarter of a circular
arc and some straight-line approximations to the arc connecting points at equally
spaced x values.
 |
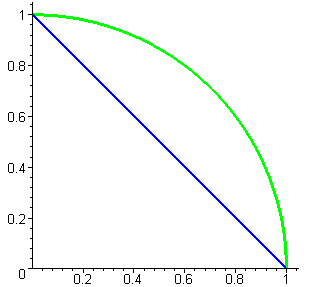Approximation with
1 line segment |
 |
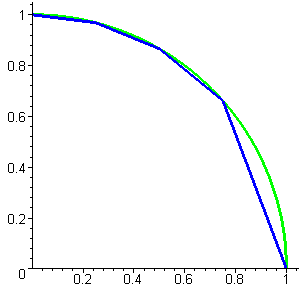Approximation with
4 line segments |
 |
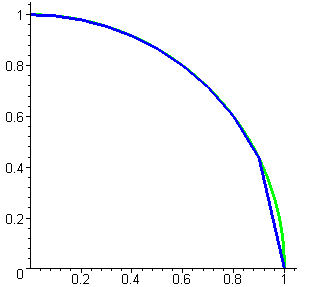Approximation with
10 line segments |
You
will calculate the work done by the force ![\begin{displaymath}\vec{F}(x,y)=\left[ \begin{array}{c} x+y \\ x-y \\ \end{array} \right] \; , \end{displaymath}](img17.gif)
on
an object moving from the point 
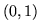to the point 
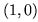along this circular arc:
- Calculate the work done if the
circular arc is approximated by one line segment and the force field is approximated
by the value of F at the start of the segment.
- Refine your estimate of the work
done by using four line segments to approximate the circular arc and four
starting points to approximate the force field.
- Refine your estimates further
by approximating the circular arc with greater numbers of line segments until
you feel confident that you have found the amount of work done.
