Vector fields and Line integrals, Part 5

Vector Fields and Line integrals

Part 5: Line Integrals

Symbolically, the sums you evaluated in Part 4 can be represented as

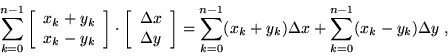
$\begin{displaymath}\sum_{k=0}^{n-1} \left[ \begin{array}{c} x_{k} + y_{k} \\ x_{k... ...y_{k})\Delta x + \sum_{k=0}^{n-1} (x_{k} - y_{k}) \Delta y \; , \end{displaymath}$

where $x_{k} = k \cdot \Delta x$ and $y_{k} = \sqrt{1 - (x_{k})^{2}}$ .

These sums are examples of Riemann sums (more specifically, left-hand Riemann sums), which are probably familiar to you as systematic ways to approximate areas under curves. (See, for example, the module on Accumulation.)

How can you alter the sum to make it a better approximation of the work done? How could you express the amount of work done symbolically in a way that is consistent with the relationship between Riemann sums and definite integrals for areas under curves? [Hint: A Riemann sum is just one sum, and the integration is with respect to just one variable.]

Let denote the circular arc joining the points and , traced out counter-clockwise. [Note that this is the opposite direction to that in Part 4.] One way to describe this arc is via a pair of parametric equations:

$\begin{displaymath}C(t)=(\gamma_{1}(t),\gamma_{2}(t)) = (1-t, \sqrt{1-(1-t)^2}) \; , \end{displaymath}$ with $0 \leq t \leq 1$ .

Use the commands in your worksheet to evaluate the following integrals:

$\begin{displaymath}\int_{0}^{1} (\gamma_{1}(t) + \gamma_{2}(t))\cdot \frac{d \gamma_{1}}{dt} dt \end{displaymath}$

$\begin{displaymath}\int_{0}^{1} (\gamma_{1}(t) - \gamma_{2}(t))\cdot \frac{d \gamma_{2}}{dt} dt \; . \end{displaymath}$

What is the sum of these integrals? How is this answer related to the work you calculated in Part 4?

Notice that the function $\gamma_{1}(t)$ specifies the -coordinate in the parametrization of the curve , and the function $\gamma2(t)$ specifies the -coordinate in the parametrization of the curve .

How are the sum $sum_{k=0}^{n-1} (x_{k} + y_{k})\Delta x$ and the integral $\int_{0}^{1} (\gamma_{1}(t) + \gamma_{2}(t))\cdot \frac{d\gamma_{1}}{dt} dt$ related? What about the sum $sum_{k=0}^{n-1} (x_{k} - y_{k})\Delta y$ and the integral $\int_{0}^{1} (\gamma_{1}(t) - \gamma_{2}(t))\cdot \frac{d\gamma_{2}}{dt} dt$ ?

In the next two steps, you will use the force $\vec{F}$ defined by the equation

$\begin{displaymath}\vec{F}(x,y)=\left[ \begin{array}{c} x + y^2 \\ x^2 - y \\ \end{array} \right] \; , \end{displaymath}$

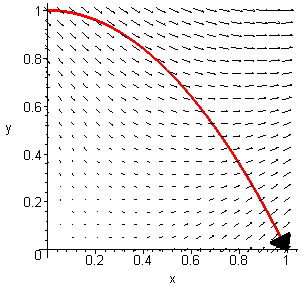
and the parabolic path along y = 1 - x² from the point to , as in the following figure.

Adapt the commands provided in your worksheet to approximate the work done when the force $\vec{F}$ acts on an object moving along the path in the direction shown. Refine your approximation until you are confident that you have found the amount of work done.
Formulate and evaluate integrals to calculate the work done when force $\vec{F}$ acts on an object moving along path in the direction shown. Compare the values of the integrals with your approximate values in step 4 for the work done.

modules at math.duke.edu