|
|
|
|
|
|
We return to the task of finishing our model for the lobster population off the Maine coast. We have only to determine a value for the environmental carrying capacity K. This will take some time. Our strategy will be to compare two different functions, each of which predicts the lobster population at the end of each year. One population function is derived from the symbolic solution to the logistic equation, and the other function is derived from our "catch" and "effort" data. We will choose the value of K will leads to the closest agreement between the two functions. This strategy is outlined in the following three steps.
A. The symbolic solution P(t) of the logistic equation, derived in part 5.3, was expressed in terms of the parameters E, P0, K, r, and Q. We will rewrite P(t) in terms of the parameter K only. Because the parameters in this function do not remain constant from year to year, it will be necessary to redefine the function each year, taking into account the yearly changes in the catch and effort. To this end, we will define a family of population functions Pop(j,K) representing the lobster population at the end of year j, given environmental carrying capacity K.
B. We can also estimate the lobster population each year using our catch and effort data along with the relationship H = QEP. Since we can express Q as a function of K, we obtain another population function which depends only on the parameter K.
C. We now compare the two models, first by "eyeballing" their closeness, and then by using a standard formula for distance between two sets of data. By experimenting, we look for the value of K yielding the smallest relative error.
A.
Let j index the years covered in our data, starting with j = 0 (1940) and going to j = 36 (1976). Then define Pop(j,K) to be the lobster population remaining at the end of year j, as predicted from our model, if the environmental carrying capacity is equal to K.
In Part 5.3 you obtained the following formula (or one equivalent to it) for the lobster population P in terms of the time variable t and the five parameters, E, P0, K, r, and Q:
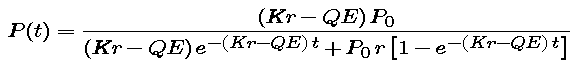
To express Pop(j,K) in terms of all these parameters requires care.
The parameters r and Q were modeled in Part 5.6 as functions of K, using the (known) slope and intercept of the linear relationship between H / E and E:
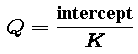
and
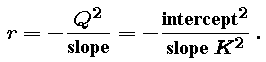
Thus, our model population at time t depends on just three parameters, E, P0, and K. We assume that each year the effort exerted by the lobstermen is as in our data, i.e., in year j the effort Ej will be the j-th entry in our effort data -- which was obtained via our model effort function from actual data on number of traps in use. And the starting population P0 we can model as a function of K from the assumption that the first year's catch is Q(K) E0 P0, so
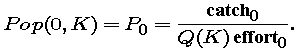
Now we have the population function expressed in terms of just the one remaining parameter, K.
Here is our strategy for constructing a model function Pop(j,K) for the population in year j, given a carrying capacity K: Each year the lobstermen's effort changes, so we must use a different solution function for each year. This means that we will always take t = 1, and each new P0 will have to be taken as the ending population of the previous year. That is, having calculated Pop(j-1,K), we move on to find Pop(j,K) as the value of P(1), with P0 replaced by Pop(j-1,K), and with the other parameters calculated from the formulas above.
B.
So far, our strategy allows us to construct a model population function for every carrying capacity K. How will we know the "best" value for K -- or even a "good" value, for that matter? Well, we have another way to estimate the lobster population in each year from the relation between population, catch, and effort: H = QEP, so we should find the population P(j) in year j to be estimated by
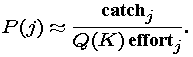
We will compare Pop(j,K) with P(j) (also dependent on K) for various values of K until we find a good fit.
The following figure shows the result of constructing our two population functions -- the model function (red) and the data-induced function (blue) -- for K = 50,000, which will be your starting point in the worksheet.
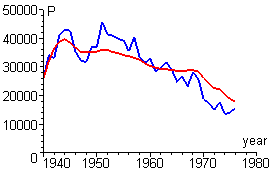
C. We illustrated comparison of the model function and the data function with
K = 50,000. You might reasonably wonder 50,000 what?
Well, it's whatever the units are for the lobster population, but we can no
longer tell what that might be. We have units for catch (metric tons),
and the catchability quotient Q is presumably a pure fraction of the
population (no units). But the other factor in our population measurements is
effort, which was defined in an arbitrary way from the number of traps
in use, so the units are now quite arbitrary. This is of no great concern, because
whatever the units are, they are consistent for comparisons of the two functions.
Steps 5 and 6 illustrate the difficulty
of "eyeballing" the goodness of fit in this situation. The model function roughly
tracks the data-induced function in both cases, even with a change in K
by a factor of 5. Thus, we need a measure of goodness of fit.
We can start by summing the squares of the deviations, Pop(j,K) - P(j).
However, just minimizing this sum is not good enough, because we need to scale
the deviations to the population itself (or to the carrying capacity) -- larger
deviations are more tolerable if all the numbers are larger. On the other hand,
we can't just scale the sum of squares by a population, because the units don't
match. If we take the square root of our sum of squares, the result will have
the same units as population. Then we can scale by K, and we will have
a "pure" measure of fit. To summarize, we want to choose K to minimize
the relative error function:
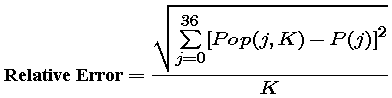
|
|
|
| modules at math.duke.edu | Copyright CCP and the author(s), 1999 |