Fourier Approximations and Music

Part 6: Fourier Approximations for General Functions of Arbitrary Period

In our discussion in Parts 2-5, we have focused on periodic functions with period 2*pi. This was because the sine and cosine functions represent the most basic periodic motions, and those functions have period 2*pi. However, most periodic functions have periods other than 2*pi. Think about the period of the pressure function corresponding to a note played on a guitar that we examined in Part 2.5.

This function has a fundamental period approximately 1/440 seconds.

In this part of the module, we will investigate how to extend our approximation strategy to include periodic functions with arbitrary periods.

As we noted previously, we used 2*pi-periodic trigonometric polynomials to approximate 2*pi-periodic functions. Now suppose we have a function that is 2L-periodic. (Even for an arbitrary period, we will find it convenient to express the period as a multiple of 2.) In particular, suppose the function we want to approximate has period 10, i.e., L = 5. So, if we look at the graph of this periodic function, it will complete one whole period on the interval from -5 to 5.

We'll begin by deciding what basic trigonometric functions should we use for our approximations in this setting.

1. Graph the function sin(t) on the interval from -pi to pi and the function sin(2*(pi/10)*t) on the interval from -5 to 5. What do you observe?

2. Graph the function cos(2t) on the interval from -pi to pi. Define and graph the corresponding 10-periodic cosine function, i.e., one that has a graph with the same shape as the graph of cos(2t) on the interval from -5 to 5.

3. Find 10-periodic functions that correspond to cos(3t) and sin(5t).

4. What is the value of w such that sin(kwt) and cos(kwt) on [-5, 5] correspond to sin(kt) and cos(kt) on [-pi, pi]?

5. Find the value of w such that sin(kwt) and cos(kwt) on [-L, L] correspond to sin(kt) and cos(kt) on [-pi, pi]. Check your answer with k = 3 and two different values of L.

6. Find the value of w so that the function f(t) = cos(wt) will have period 1/440 of a second.

Based on our what we have learned in Steps 1-6, we will approximate 2L periodic functions with trigonometric polynomials built up from constant terms a₀ and terms of the form

a_k cos(k(pi/L)t) and b_ksin(k(pi/L)t), where k = 1, 2, 3, ...

The question now is how to define and calculate the coefficients a₀, a_k , and b_k in this general setting.

7. If f is a 2*pi-periodic function, then
   

   Give a geometrical interpretation of the value of a₀, i.e., what are you finding when you integrate a function over an interval and divide the result by the length of the interval?

8. Write down the corresponding formula for a₀ in the case that f is a 2L-periodic function.

If f is a 2*pi-periodic function, we know that

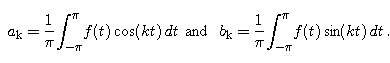
The 1/pi factor in the front of the integrals resulted from the calculations

9. Evaluate the integrals
   

   by using a substitution to transform the integrals to ones previously evaluated. Use your symbolic algebra system to verify your calculations.

From this information, we may construct the approximating polynomials

or

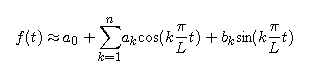
using the formulas

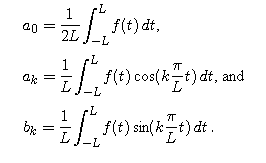
Now we examine the approximations of periodic functions of arbitrary period obtained using these trigonometric polynomials.

10. Let f be the function defined by
    f(t) = t² for t between -1 and 1

    and extended to be periodic of period 2. Construct the approximating polynomials, and compare the graphs of the polynomials to the graph of the original function.

11. Let f be the function defined by
    f(t) = t for t between -1/220 and 1/220

    and extended to be periodic of period 1/110. Construct the approximating polynomials, and compare the graphs of the polynomials to the graph of the original function.

Sometimes the "natural" domain of a periodic function is not an interval that is symmetric about the origin. For example, in the next part of this module, we will consider the periodic variations in the Canadian lynx population during the 19^th century. Here, a natural periodic interval of the population as a function of time is the interval between the years 1821 to 1861. We now consider how to go about defining approximating trigonometric polynomials in this case.

To be more precise, suppose that we can tell that a function f is periodic and that it completes one fundamental variation over the interval [c, d]. Thus f is periodic with period d - c and not periodic with any shorter period.

12. Write the integral formulas for the coefficients a₀, a_k and b_k of the approximating polynomials in terms of c, d, and L = (d - c)/2.

13. Let f be the function defined by
    f(t) = exp(t/3) for t between 1 and 4

    and extended to be periodic of period 3. Construct the approximating polynomials, and compare the graphs of the polynomials to the graph of the original function. Show at least three such comparisons.

---

modules at math.duke.edu

Copyright CCP and the author(s), 1998, 1999