The One-Dimensional Wave Equation

Part 2: Fourier Series Form of Solutions

Now we consider the Fourier series form of the solution of the initial/boundary value problem

Again the function f has the graph

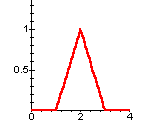
1. We know that the the solution of this problem may be approximated by functions A of the form
   
   where the coefficients c_k are given by
   .
   Calculate the coefficients c_k.

2. We know that sums of the form
   approximate the function f. Compare the graph of f with the graphs of the approximations to f for n = 1, 2, ..., 15.

3. Using n = 15, calculate the approximation A(x,t) to y(x,t), and compare the graph of the traveling wave solution with the graph of the approximation A, both as functions of x, for specific values of t between 0 and 8.