The One-Dimensional Wave Equation
Part 3: Non-Zero Initial Velocity
Now we consider a boundary/initial value problem with non-zero initial velocity t.

Here the initial position function f is the same as before
Graph of f
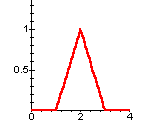
The initial velocity function g has the graph shown below.
Graph of g

We know that, in this case, the solution y(x,t) of the initial/boundary value problem may be approximated by
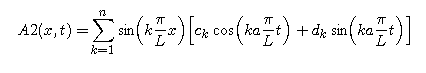
Here, the half-range Fourier sine approximations to g are
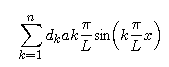 .
.
Thus, the coefficients dk are given by
![Formula for d[k]](figure15.gif) .
.
- Calculate the coefficients dk, and check the half-range approximations to g.
- Graph the approximation A2 to the solution of the initial/boundary value problem as a function of x for a range of values of t between 0 and 8. How does the solution of this problem differ from the one with zero initial velocity?



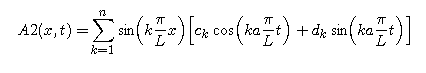
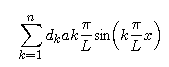 .
.![Formula for d[k]](figure15.gif) .
.